Coursera.org 机器学习 笔记
These are the notes by learning Andrew Ng’s “Machine Learning” from Coursera.org for future review

• Machine Learning
  • Introduction
• Machine Learning Algorithms
  • Supervised learning
  • Unsupervised learning
  • Model representation
  • Cost function
  • Gradient descent
• Multivariate Linear Regression
  • Multiple Features (variables)
  • Normal equation
• Classification
  • Logistic Regression
• Overfitting
  • Regularization
  • Logistic Regression
• Neural Networks
  • Model representation(NN)
• To be continued

Machine Learning

• Grew out of work in AI
• New capability for computers

Examples:

Database mining
Large datasets from growth of automation/ web
E.g., Web click data, medical records, biology, engineering

Applications cannot program by hand
E.g., Autonomous helicopter, handwriting recognition, most of Natural Language Processing (NLP), Computer Vision

Self-customizing programs
E.g., Amazon, Netflix product recommendations

Understanding human learning (brain, real AI)

Introduction

• Definition
  • Arthur Samuel (1959). Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed
  • Tom Mitchell (1995) Well-posed Leaning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

Machine Learning Algorithms:

Supervised learning

• “Right answers” given
• Regression: Predict continuous valued output
• Classification: Discrete valued output (0 or 1 or others)

Unsupervised learning

• allows us to approach problems with little or no idea what our results should look like.
• We can derive structure from data where we do not necessarily know the effect of the variables.
• We can derive this structure by clustering the data based on relationships among the variables in the data

• There is no feedback based on the prediction results

• E.g., Organize computing clusters, social network analysis, market segmentation, astronomical data analysis

Model representation

• Notation
  • m = Number of training examples
  • x’s = “input” variable / features
  • y’s = “output” variable / “target” variable
• Hypothesis
  • Training set → Learning Algorithm → Hypothesis (h)
  • x → h → estimated value of y
  • h: X → Y
  • h maps x’s to y’s
  • Linear regression with one variable or Univariate linear regression
  • $ h_{\theta}(x) = \theta_{0} + \theta_{1}x $
  • shorthand: $ h(x) $
  • $ \theta_{i} $’s: parameters

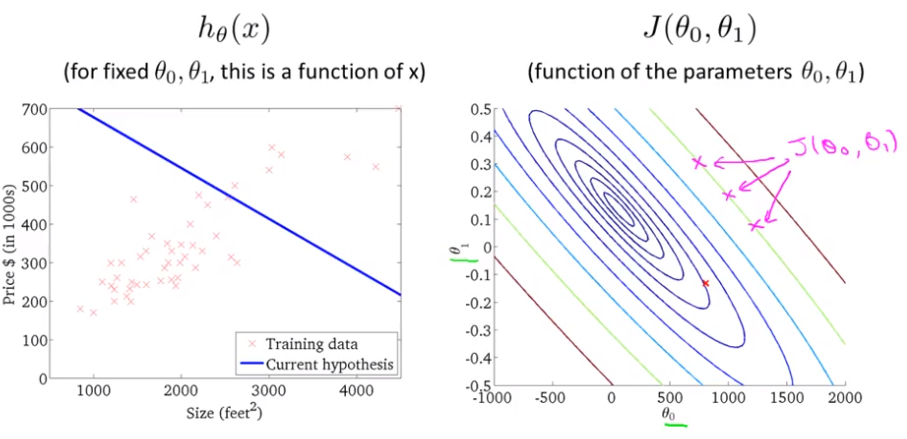
Cost function

• Idea: Choose $ \theta_{0}, \theta_{1} $ so that $ h_{\theta}(x) $ is close to y for our training examples (x,y)
  • $ \underset{ \theta_{0}, \ \theta_{1} }{ \mathrm{minimize} } $ $ \dfrac{1}{2m} \displaystyle\sum_{i=1}^m ( \hat{y}^{i}- y^{i} )^2 = $ $\dfrac{1}{2m} \displaystyle\sum _{i=1}^m (h_\theta (x^{i}) - y^{i} )^2$
  • $ h_{\theta}(x^{i}) = \theta_{0} + \theta_{1}x^{i} $
• Cost function: $ J(\theta_0, \theta_1) = $ $\displaystyle \dfrac{1}{2m} \sum _{i=1}^m ( \hat{y}^{i}- y^{i} )^2 = \dfrac{1}{2m} \sum _{i=1}^m (h_\theta (x^{i}) - y^{i} )^2$
  • Octave: J = 1/(2*m)*sum((X*theta .- y).^2)
  • also called squared error cost function or squared error function

• Goal: $ \displaystyle \underset{ \theta_{0}, \ \theta_{1} }{ \mathrm{minimize} } J(\theta_0, \theta_1) $

• contour plots or contour figures：
  

Gradient descent

• Outline:
  • Start with some $ \theta_{0}, \ \theta_{1} $
  • Keep changing $ \theta_{0}, \ \theta_{1} $ to reduce $ J(\theta_{0}, \theta_{1}) $ until we hopefully end up at a minimum
• Algorithm
  • repeat until convergence { $ \theta_j := \theta_j - \alpha \displaystyle \frac{\partial}{\partial \theta_j} J(\theta_0, \ \theta_1) \ \ (\mathrm{for} \ j = 0 \ \mathrm{and} \ j = 1 ) $ }
  • α: learning rate: too small → slow ; too large → overshoot; proper → automatically decrease α over time
  • Correct simultaneous update
    • temp0 := $ \theta_0 - \alpha \displaystyle \frac{\partial}{\partial \theta_0} J(\theta_0, \ \theta_1) \ \ (\mathrm{for} \ j = 0 \ \mathrm{and} \ j = 1 ) $
    • temp1 := $ \theta_1 - \alpha \displaystyle \frac{\partial}{\partial \theta_1} J(\theta_0, \ \theta_1) \ \ (\mathrm{for} \ j = 0 \ \mathrm{and} \ j = 1 ) $
    • $ \theta_0 := $ temp0
    • $ \theta_1 := $ temp1
  • linear regression:
    • repeat until convergence:
    • $ \theta_0 := \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}(h_\theta(x_{i}) - y_{i}) $
    • $ \theta_1 := \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}((h_\theta(x_{i}) - y_{i}) x_{i})$
    • Octave: theta = theta - alpha/m*(X'*(X*theta .- y))
• “Batch” Gradient Descent:
  • “Batch”: Each step of gradient descent uses all the training examples

Multivariate Linear Regression

Multiple Features (variables)

• n = number of features
• $ x^{(i)} \text{ for } (i\in { 1,\dots, m } ) $ = input (features) of $ i^{th} $ training examples
  • $ x^{i} = [ x_{1}^{i} \ x_{2}^{i} \ \dots \ x_{n}^{i} ]^{T} \in \mathbb{R}^{n} $
• $ x_{j}^{(i)} $ = value of $ j^{th} $ features in $ i^{th} $ training examples
• Hypothesis: $h_{\theta}(x^{i}) = \theta_{0} + \theta_{1}x_{1}^{i} + \theta_{2}x_{2}^{i} + \dots + \theta_{n}x_{n}^{i}$
  • $ x = [ x_{0} \ x_{1} \ x_{2} \ \dots \ x_{n} ]^{T} \in \mathbb{R}^{n+1} \ \ (x_{0}^{i} = 1) $
  • $ \theta = [ \theta_{0} \ \theta_{1} \ \theta_{2} \ \dots \ \theta_{n} ]^{T} \in \mathbb{R}^{n+1} $
  • $ h_{\theta}(x) = \theta_{0}x_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + \dots + \theta_{n}x_{n} \ \ (x_{0} = 1) $
    $ \ \ \ \ \ = \theta^{T}x $
• Parameters: $ \theta_{0}, \theta_{1}, \dots , \theta_{n} $
• Cost function: $ J(\theta) = J(\theta_{0}, \theta_{1}, \dots , \theta_{n}) = $ $\dfrac{1}{2m} \displaystyle\sum_{i=1}^m (h_\theta (x^{i}) - y^{i} )^2$
  $\hspace{3em} J(\theta) = \dfrac{1}{2m} \displaystyle\sum_{i=1}^{m}((\sum_{j=0}^{n}\theta_j x^{(i)}_j) - y^{(i)})^2$
• Gradient descent:
  Repeat {
  $\theta_j := \theta_j - \alpha \displaystyle \frac{\partial}{\partial \theta_j} J(\theta)$
  } (simultaneously update for every $ j = 0, \dots, n $ )

• New algorithm (n ≥ 1):
  Repeat {
  $\theta_j := \theta_j - \alpha \displaystyle \frac{1}{m} \sum\limits_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_{j}^{(i)}$
  } (simultaneously update $ \theta_j $ for $ j = 0, \dots, n $ )

• Features Scaling
  • Let $ x = \displaystyle \frac{x}{ \mathrm{range} S } $
    to get every feature into approximately a $ -1 \leq x \leq 1 $ range
  • Mean normalization: replace $ x_j \mathrm{with} \frac{x_j - \mu_j}{ s_{j} } $ (Do not apply to $ x_0 = 1 $)
    into $ -0.5 \leq x_j \leq 0.5 $ range
• Learning Rate choose
  • “Debugging”: plot ( $ \displaystyle\underset{ \theta }{ \mathrm{min} } \ J(\theta) $, No. of iterations)
    $ J(\theta) $ should decrease after every iteration → converge (sufficiently α)
  • Not working → Use smaller α
    slow converge → use larger α
• Create new feature
• Change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function or any other form (Features Scaling)

Normal equation

• Definition: Method to solve for θ analytically
• Formula: $ \displaystyle\theta = (X^{T} X)^{-1} X^{T} y $
  • Octave: pinv(x'*x)*x'*y
  • No need feature scaling
  • If n is very large, it works very slow, by compute $ n^3 $

Classification

• Binary classification problem: y = 0 or 1
• Use linear regression:
  • To map all predictions greater than 0.5 as a 1 and all less than 0.5 as a 0
  • $ h_\theta(x) $ can be >1 or <0, so it does not work well
• Logistic Regression: make $ 0 \le h_\theta(x) \le 1 $

Logistic Regression

• Clasification and Representation
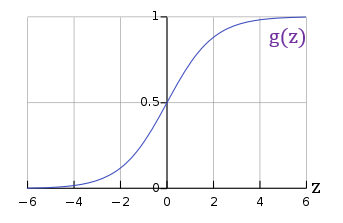
  • Sigmoid(Logistic) function: $ g(Z) = \displaystyle\frac{1}{1+e^{-z}} $
  • Octave: h = 1.0 ./ (1.0 + exp(-z))
  • $ h_\theta(x) = g(\theta^{T}x) = \displaystyle\frac{1}{1+e^{-\theta^{T}x}} $
    
  • $ h_\theta(x) = $ estimated probability that y = 1 on input x
  • $ h_\theta(x) = P(y=1 \vert x ; \theta) = 1 - P(y=0 \vert x ; \theta) $
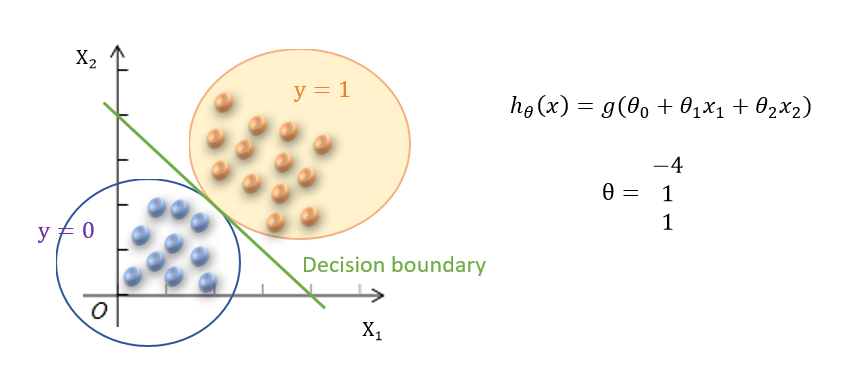
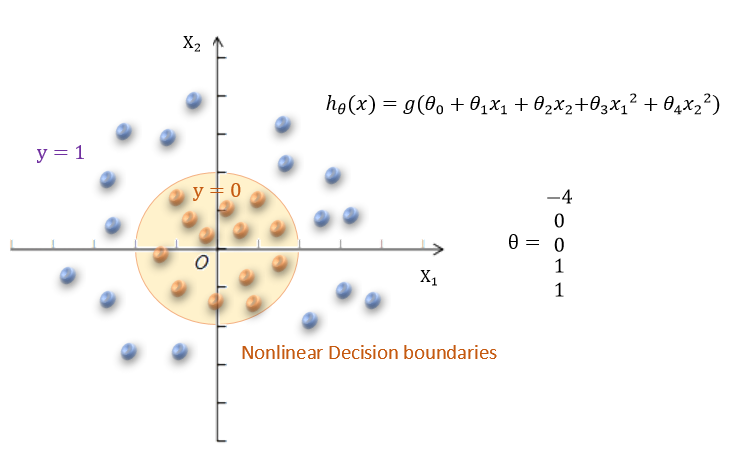
• Decision boundary
  • To get discrete 0 or 1 classification, can translate the output of the hypothesis function as:
    • $ h_\theta(x) \geq 0.5 \rightarrow y = 1 $
    • $ h_\theta(x) \leq 0.5 \rightarrow y = 0 $
  • $ g(z) \geq 0.5 $ when $ z \geq 0 $ that $ h_\theta(x) = g(\theta^T x) \geq 0.5 $ when $ \theta^T x \geq 0 $
  • From these statements we can say:
    • $ \theta^T x \geq 0 \Rightarrow y = 1 $
    • $ \theta^T x \leq 0 \Rightarrow y = 0 $
      
      
• Cost function
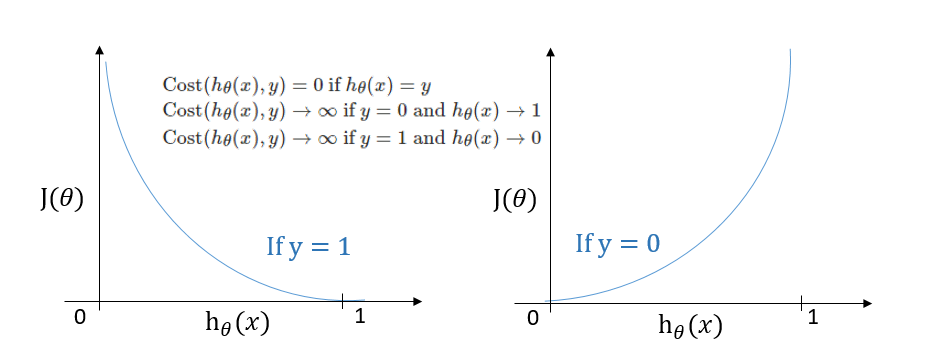
  • $ J(\theta) = \displaystyle\dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) $
  • $ \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) $ if y = 1
  • $ \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) $ if y = 0
    
  • Compress: $ \displaystyle \mathrm{Cost}(h_\theta(x),y) = -y\log(h_\theta(x)) -(1-y)\log(1-h_\theta(x)) $
  • Vectorized implementation:
    $ h = g(X\theta) $
    $ \displaystyle J(\theta) = \frac{1}{m} \cdot (-y^{T}\log(h)-(1-y)^{T}\log(1-h)) $
    Octave: the cost: J = 1/m * (-y' * log(h)-(1-y)'*log(1-h))
    the partial derivatives: grad = 1/m * X'*(h-y)
• Gradient Descent
  • Repeat {
    general form:
    $ \displaystyle \theta_j := \theta_j - \alpha \dfrac{\partial}{\partial \theta_j}J(\theta) $
    derivative part using calculus:
    $ \displaystyle \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} $
    }
  • Vectorized implementation:
    $\displaystyle \theta := \theta - \frac{\alpha}{m} X^T (g(X\theta) - \vec y) $
• Optimization algorithm
  • Gradient Descent
  • Conjugate gradient
  • BFGS
  • L-BFGS
• Codes in Octave:
  function [jVal, gradient] = costFunction(theta)
jVal = [...code to compute J(theta)...];
gradient = [...code to compute derivative of J(theta)...]; end
  • use octave’s ‘fminunc’ optimization algorithm
    options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
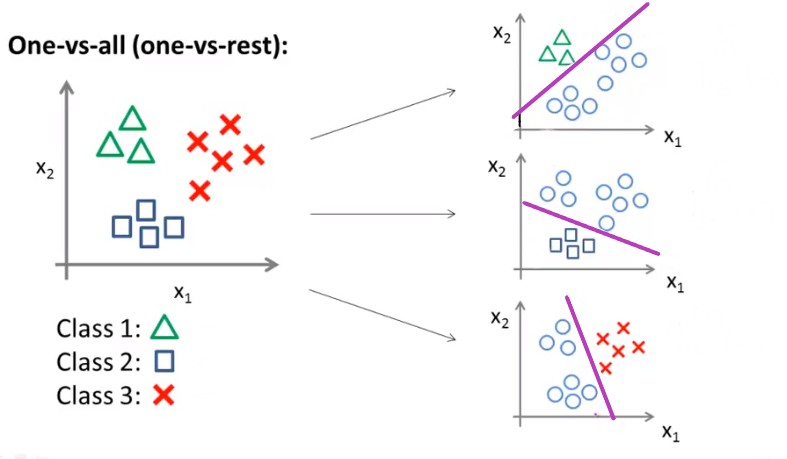
• Multiclass Classification: One-vs-all
  • Train a logistic regression classifier $h_\theta^{(i)}(x)$ for each class i to predict the probability that $y = i$
    $ h_\theta^{(i)}(x) = P(y = i| x;\theta) (i=1,2,\dots,n) $
  • On a new input x, to make a prediction, pick the class i that maximizes
    prediction = $ \displaystyle\underset{i}{\mathrm{max}} h_\theta^{(i)}(x) $
    

Overfitting

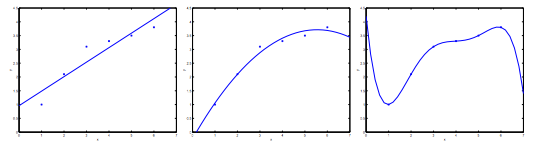
• “Underfit” (“high bias”): not fit the training data very well
• “Just right”
• “Overfit” (“high variance”): may fit the trainning set very well, but fail to generalize to new examples

Regularization

• Using the cost function with the extra summation, we can smooth the output of our hypothesis function to reduce overfitting.
  $ min_\theta\, \dfrac{1}{2m}\, \displaystyle[\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2] $
• $\lambda$, or lambda is the regularization parameter
• If lambda is too large, it may cause underfitting.

Linear Regression

• Gradient Descent:
  Repeat {
  $ \displaystyle\theta_0 := \theta_0 - \alpha\, \frac{1}{m} \displaystyle\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} $
  $ \displaystyle\theta_j := \theta_j - \alpha\, [ ( \frac{1}{m}\, \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}) + \frac{\lambda}{m}\theta_j ] $ $ \displaystyle\quad j \in \lbrace 1,2…n\rbrace $
  $ \displaystyle\Rrightarrow \theta_j := \theta_j (1- \alpha\,\frac{\lambda}{m}) - \alpha\, \frac{1}{m}\, \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}) $
  }

• Normal Equation:
  $ \displaystyle\theta = ( X^TX + \lambda \cdot L )^{-1} X^Ty $
  $ \text{where}\, \, L = $ $\begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & 1 & & \newline & & & \ddots & \newline & & & & 1 \end{bmatrix}$

Logistic Regression

• Cost function:
  • $ J(\theta) = - \displaystyle\frac{1}{m} \sum_{i=1}^m [ y^{(i)}\, \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\, \log (1 - h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 $
  • $ \sum_{j=1}^n \theta_j^2 $ means to explicitly exclude the bias term $ \theta_0 $
  • Octave:
    • the cost:
      J = 1/m * (-y' * log(h)-(1-y)'*log(1-h)) + (lambda/(2*m))*theta'*theta
    • the partial derivatives:
      grad = 1/m * X'*(h-y) + (lambda/m)*theta
• Gradient descent:
  • $ \displaystyle h_\theta(x) = \frac{1}{1+e^{-\theta^{T}x}} $
    Repeat {
    $ \displaystyle\theta_0 := \theta_0 - \alpha\, \frac{1}{m} \displaystyle\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} $
    $ \displaystyle\theta_j := \theta_j (1- \alpha\,\frac{\lambda}{m}) - \alpha\, \frac{1}{m}\, \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}) $ $ \displaystyle\quad j \in \lbrace 1,2…n\rbrace $
    }

Neural Networks

• Origins: Algorithms that try to mimic the brain

Model representation(NN)

• Neuron model: Logistic unit
  $\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline \end{bmatrix}\rightarrow\begin{bmatrix}\ \ \ \newline \end{bmatrix}\rightarrow h_\theta(x)$
  • Sigmoid (logistic) activation function: $ g(Z) = \displaystyle\frac{1}{1+e^{-z}} $
  • Parameters $ \theta $ also called “weights”
    
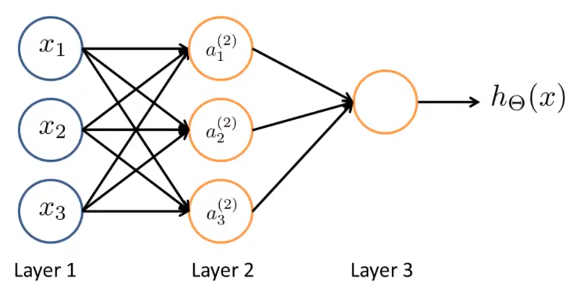
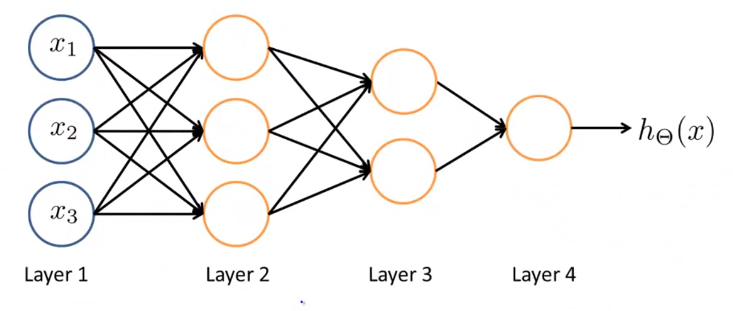
  • 1st layer called “input layer”; last layer called “output layer”; middle layers called “hidden layer”
• Notations
  • $ x_0 = 1 $ is a “bias unit”
    $\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline x_3\end{bmatrix}\rightarrow\begin{bmatrix}a_1^{(2)} \newline a_2^{(2)} \newline a_3^{(2)} \newline \end{bmatrix}\rightarrow h_\theta(x)$
  • $ a_i^{(j)} = $ “activation” of unit $ i $ in layer $ j $
  • $ \Theta^{(j)} = $ matrix of weights controlling function mapping from layer $ j $ to layer $ j+1 $

  $\begin{align*} \displaystyle a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \newline a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \newline a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \newline h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) \newline \end{align*}$

  • If network has $ s_j $ units in layer $ \displaystyle j, s_{j+1} $ units in layer $ j + 1 $, then $ \Theta^{(j)} $ will be of dimension $ \displaystyle s_{j+1} \times (s_j + 1) $ that
    $\Theta^{(j)} \in \displaystyle\Re^{s_{(j+1\ )}\ \times (s_j \ + 1)}$
• Forward propagation: Vectorized implementation
  $\displaystyle z_k^{(2)} = \Theta_{k,0}^{(1)}\ x_0 + \Theta_{k,1}^{(1)}\ x_1 + \cdots + \Theta_{k,n}^{(1)}\ x_n$
  $\begin{align*}\displaystyle x = \begin{bmatrix}x_0 \newline x_1 \newline\cdots \newline x_n\end{bmatrix} &z^{(j)} = \begin{bmatrix}z_1^{(j)} \newline z_2^{(j)} \newline\cdots \newline z_n^{(j)}\end{bmatrix}\end{align*}$
  • $ a^{(1)} = x $
  • $ \displaystyle z^{(j)} = \Theta^{(j-1)} \ a^{(j-1)} $
    $\begin{align*}\displaystyle a_1^{(2)} = g(z_1^{(2)}) \newline a_2^{(2)} = g(z_2^{(2)}) \newline a_3^{(2)} = g(z_3^{(2)}) \newline \end{align*}$
  • $ \hookrightarrow \displaystyle a^{(j)} = g(z^{(j)} ) $
  • Add $ \displaystyle a_0^{(j)} = 1 $
  • $ z^{(j+1)} = \Theta^{(j)} a^{(j)} $
  • $ \displaystyle h_\Theta(x) = \ a^{(j+1)} = \ g(z^{(j+1)}\ ) $
• Other network architectures
  

To be continued

• others: Reinforcement learning, recommender systems

• Practical advice for applying learning algorithms