Most notes and code are from:
Data Visualization

• 1. Univariate Plotting
  • 1.1. Bar Chart
  • 1.2. Line Chart
  • 1.3. Area Chart
  • 1.4. Histogram Chart
• 2. Bivariate Plotting
  • 2.1. Scatter Plot
  • 2.2. Hexplot
  • 2.3. Stacked Plots
  • 2.4. Bivariate Line Chart
• 3. Seaborn Plotting
  • 3.1. Trends
  • 3.2. sns.countplot
  • 3.3. sns.lineplot
  • 3.4. Relationship
  • 3.5. sns.barplot
  • 3.6. sns.heatmap
  • 3.7. sns.regplot
  • 3.8. sns.lmplot
  • 3.9. sns.swarmplot
  • 3.10. Distribution
  • 3.11. sns.distplot
  • 3.12. sns.kdeplot
  • 3.13. sns.jointplot
  • 3.14. sns.boxplot
  • 3.15. Themes
• 4. Seaborn Faceting
  • 4.1. Facet Grid
  • 4.2. Pair Plot
• 5. Multivariate Plotting
  • 5.1. Grouped box plot
  • 5.2. Heatmap
  • 5.3. Parallel Coordinates
• 6. Plotly
  • 6.1. go Scatter
  • 6.2. go Heatmap
  • 6.3. go Choropleth
  • 6.4. go Surface
• 7. Grammar of Graphics
  • 7.1. Scatter plot
  • 7.2. Add regression line
  • 7.3. Add color
  • 7.4. Add facet
  • 7.5. Aes
  • 7.6. Bar plot
  • 7.7. histogram
  • 7.8. 2D histogram
• 8. Time-series plotting
  • 8.1. Lag plot
  • 8.2. Autocorrelation plot

import pandas as pd
import re
import numpy as np
pd.set_option('max_columns', None) # show the max columns
df is the dataset
'X' is the X-axis name
'Y' is the y-axies name

1. Univariate Plotting

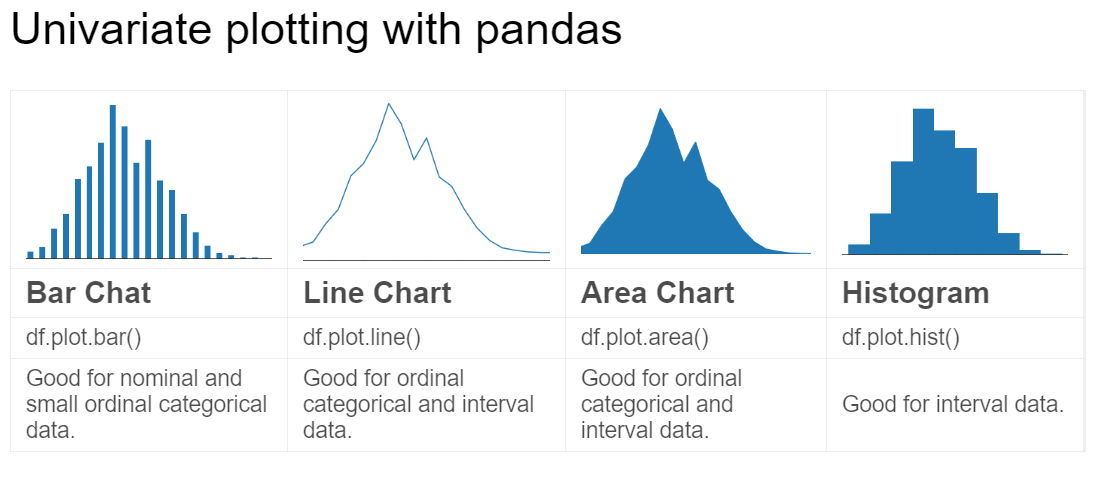
1.1. Bar Chart

• Y is the total amount counts of each X
  • df['X'].value_counts().head(10).plot.bar()
• Y is the proportions of each X
  • (df['X'].value_counts().head(10) / len(df)).plot.bar()
• Sort the ordinal categories X
  • df['X'].value_counts().sort_index().plot.bar()

1.2. Line Chart

• Sort the ordinal categories X
  • df['X'].value_counts().sort_index().plot.line()

1.3. Area Chart

• Sort the ordinal categories X
  • df['X'].value_counts().sort_index().plot.area()

1.4. Histogram Chart

• Deal with the skewed data and limit up to 200
  • df[df['X'] < 200]['X'].plot.hist()
• Basic histogram chart
  • df['X'].plot.his()

2. Bivariate Plotting

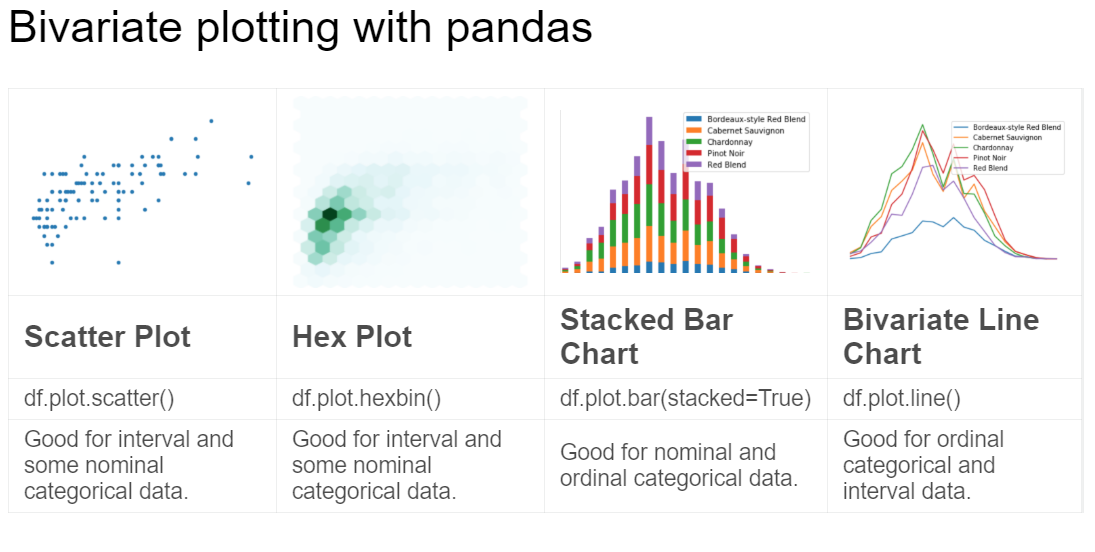
2.1. Scatter Plot

This map is often used to show the correlation between two variables
It works best with a mixture of ordinal categorical and interval data.

• Map X to Y in 2_D space (limit X up to 100)
  • df[df['X'] < 100].sample(100).plot.scatter(x = 'X', y = 'Y')
  • To downsample data is also important to prevent overplotting

2.2. Hexplot

• Hexplot is a way to deal with overplotting
  • 'df[df['X']<100].plot.hexbin(x='X',y='Y', gridsize = 15)

2.3. Stacked Plots

Often with nominal categorical data

• Reform the data with the groupby X to counts amount y with 2 variables
  • reform_df = df.groupby(['X_1','X_2']).mean()[['variable_1','variable_2']]
• Dealing with the probelm: one categorical variable in the columns, one categorical variable in the rows, and counts of their intersections in the entries
  • df.plot.bar(stacked=True) in bar plots
  • df.plot.area() in area plots

2.4. Bivariate Line Chart

Better with interval data

• Reform the data with the groupby X to counts amount y with 4 variables
  • reform_df = df.groupby(['X']).mean()[['v_1','v_2','v_3','v_4']]
• Multiple lines on the same chart
  • df.plot.line()

3. Seaborn Plotting

import seaborn as sns is a standalone data visualization package

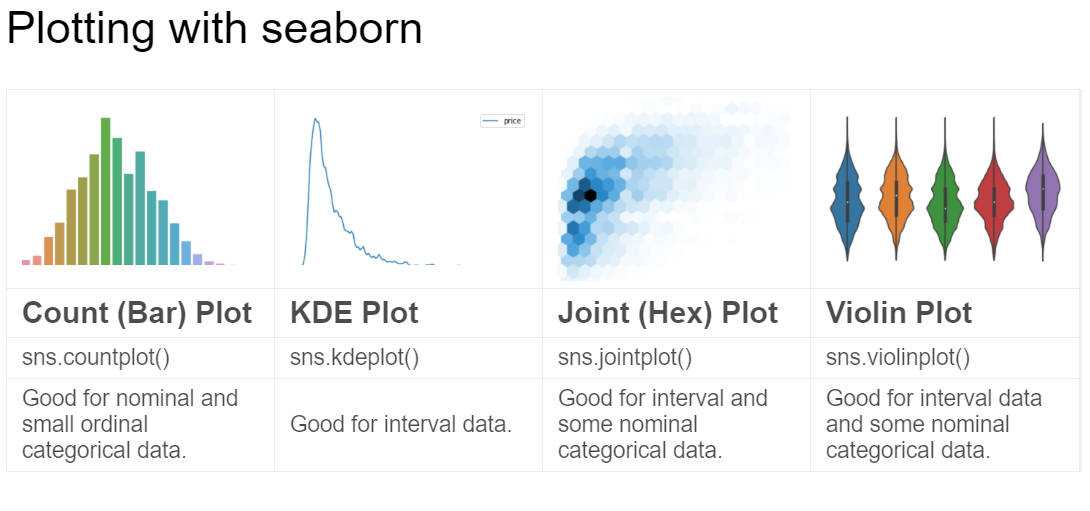
3.1. Trends

A trend is defined as a pattern of change.

3.2. sns.countplot

• Same as pandas’ value_counts which is equivalent bar plot
  • sns.countplot(df['X'])

3.3. sns.lineplot

• Line charts are best to show trends over a period of time, and multiple lines can be used to show trends in more than one group.

3.4. Relationship

There are many different chart types that you can use to understand relationships between variables in your data.

3.5. sns.barplot

• Bar charts are useful for comparing quantities corresponding to different groups.

3.6. sns.heatmap

• Heatmaps can be used to find color-coded patterns in tables of numbers. sns.scatterplot - Scatter plots show the relationship between two continuous variables; if color-coded, we can also show the relationship with a third categorical variable.

  ef = (df.loc[:,['Val_1','Val_2','Val_3','Val_4','Val_5']].applymap(lambda v: int(v) if str.isdecimal(v) else np.nan).dropna()).corr()  
  sns.heatmap(ef, annot = True)  
  

3.7. sns.regplot

• Including a regression line in the scatter plot makes it easier to see any linear relationship between two variables.

3.8. sns.lmplot

• This command is useful for drawing multiple regression lines, if the scatter plot contains multiple, color-coded groups.

    sns.lmplot(x='X', y='Y', hue='Val', markers=['o', 'x', '*'], data = df.loc[df['Val']isin(['val_1','val_2','val_3'])], fit_reg=False)
  

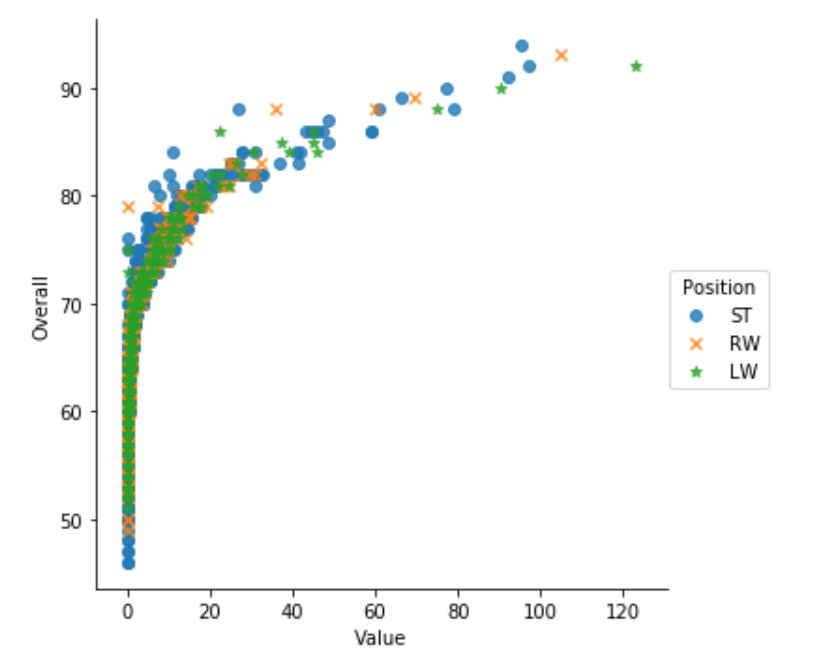
3.9. sns.swarmplot

• Categorical scatter plots show the relationship between a continuous variable and a categorical variable.

3.10. Distribution

We visualize distributions to show the possible values that we can expect to see in a variable, along with how likely they are.

3.11. sns.distplot

• Histograms show the distribution of a single numerical variable.
  • sns.distplot(df['X'],bins=10,kde=False) number of bins to 10

3.12. sns.kdeplot

• KDE “kernel density estimate” plots (or 2D KDE plots) show an estimated, smooth distribution of a single numerical variable (or two numerical variables).
• y axis in this case is how often it occurs
  • sns.kdeplot(df.query('X < 200').X)
• KDE plots in 2-D (Bivariate KDE)
  • sns.kdeplot(df[df['X']<200].loc[:,['X','Y']].dropna().sample(5000))
  • sns.kdeplot(df['X'],df['Y'])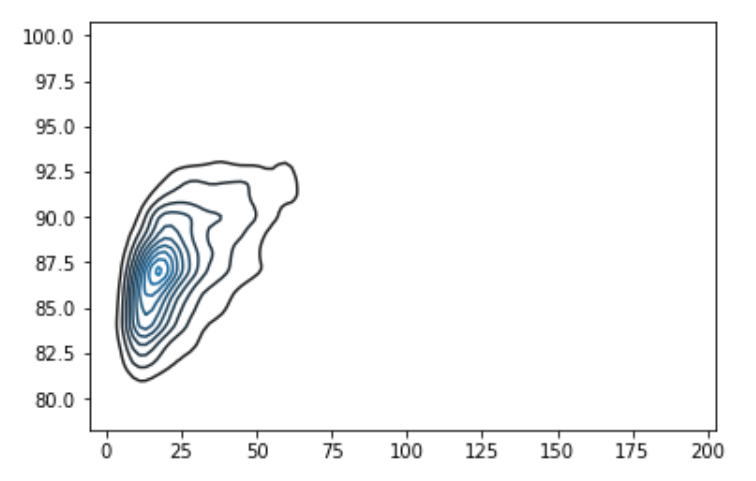
  • 

3.13. sns.jointplot

• This command is useful for simultaneously displaying a 2D KDE plot with the corresponding KDE plots for each individual variable.
  • sns.jointplot(x='X',y='Y',data=df[df['X']<100])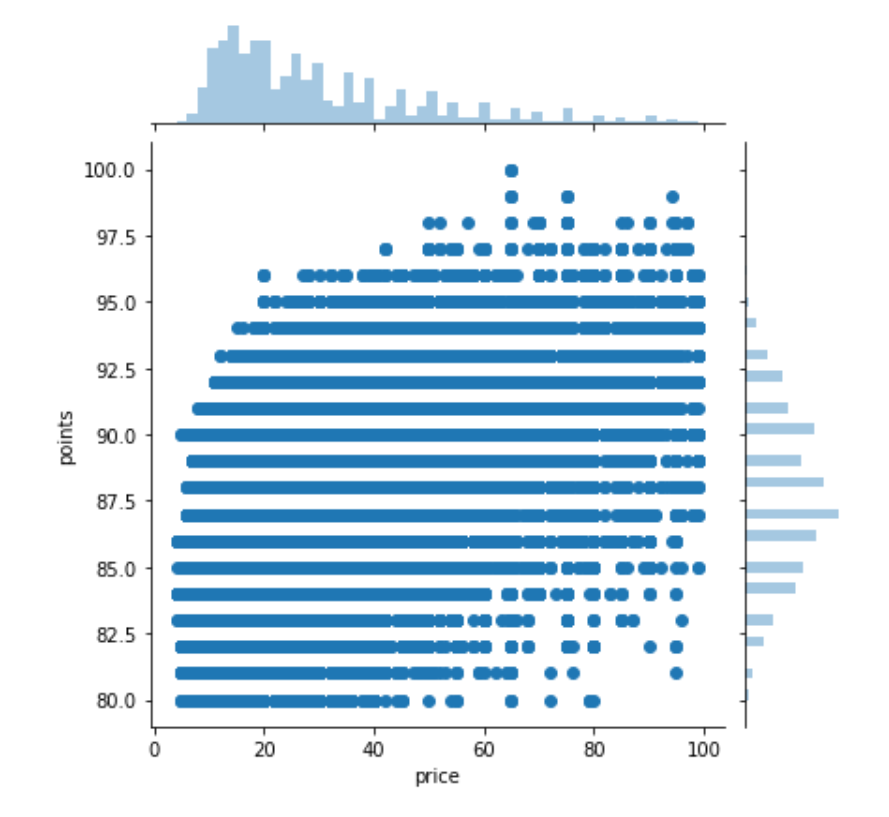
  • 
  • sns.jointplot(x='X',y='Y',data=df[df['X']<100],kind='hex',gridsize=20)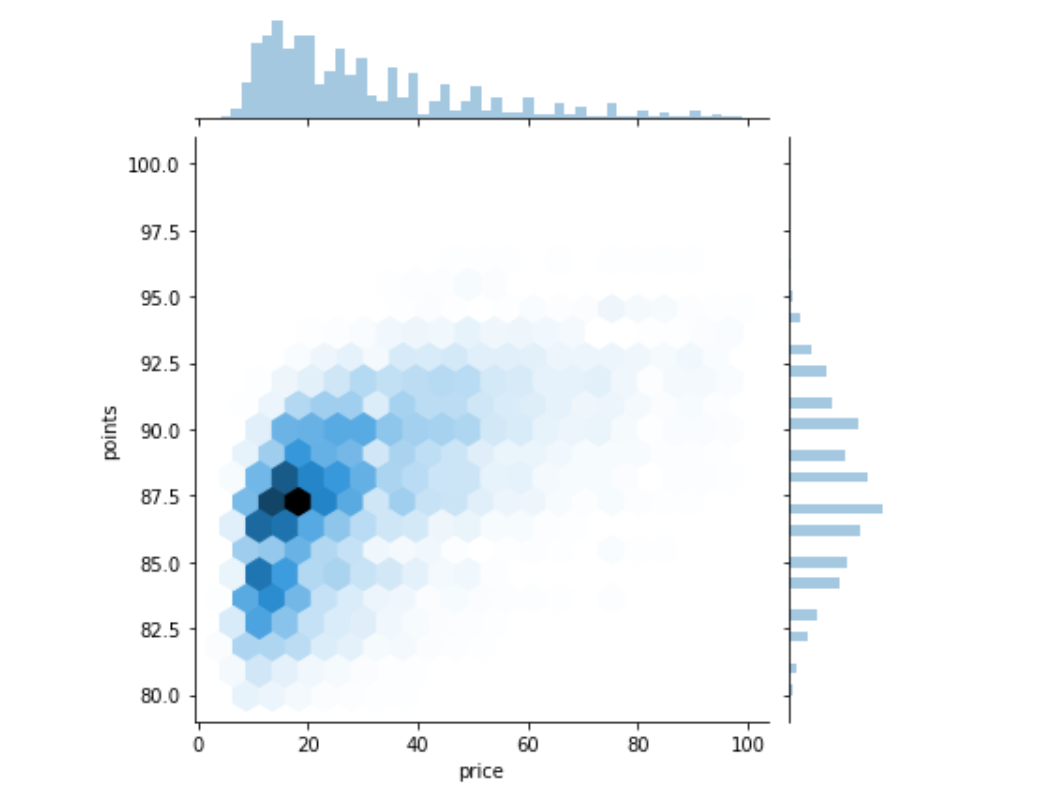
  • 

3.14. sns.boxplot

• Boxplot is great for summarizing the shape od may datasets

    sns.boxplot(
    	x='X',
    	y='Y',
    	data=df[df.X.isin(df.X.value_counts().head(5).index)]
        )
  

• Violin Plot cleverly replaces the box in the boxplot with a kernel density estimate for the data

    sns.violinplot(
    	x='X',
    	y='Y',
    	data=df[df.X.isin(df.X.value_counts()[:5].index)]
        )
  

3.15. Themes

• Seaborn has five different themes: (1)”darkgrid”, (2)”whitegrid”, (3)”dark”, (4)”white”, and (5)”ticks”

sns.set_style("dark")

4. Seaborn Faceting

Faceting is the act of breaking data variables up across multiple subplots, and combining those subplots into a single figure
It’s a multivariate technique which is very easy to use

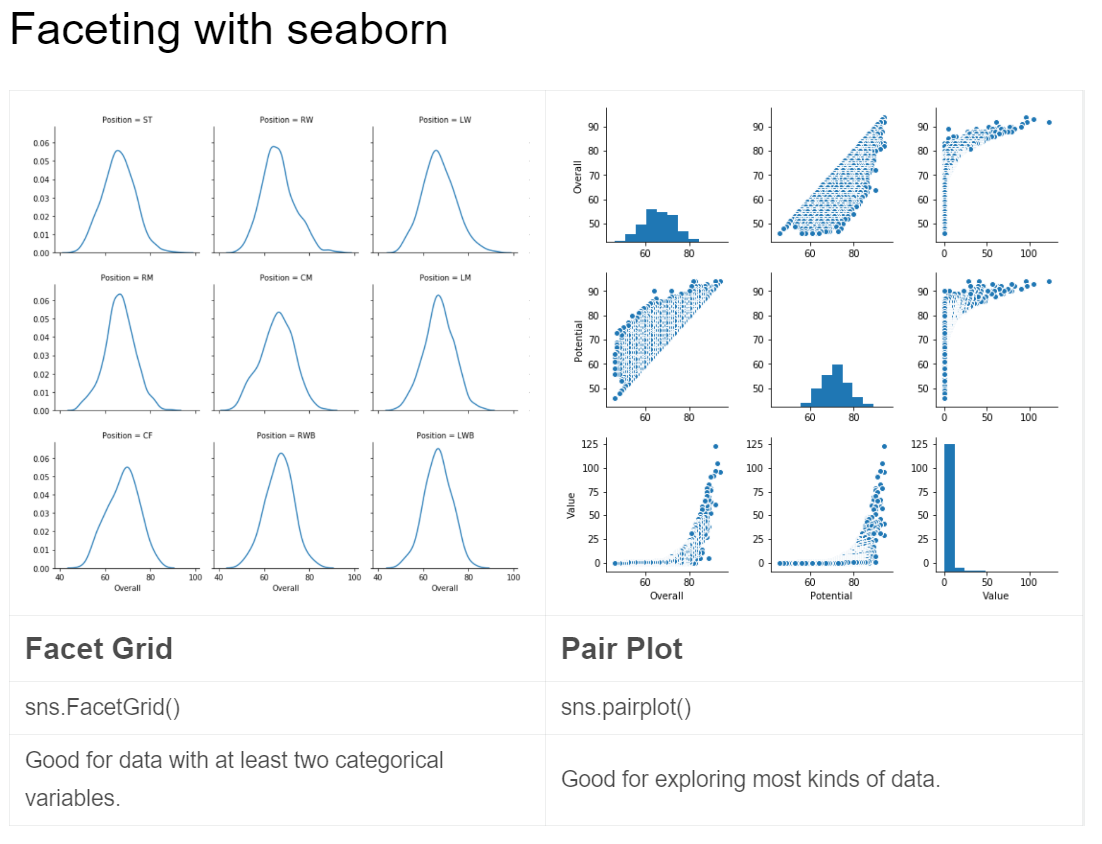
4.1. Facet Grid

Vals are the df.columns()
vals are the subconditions under the columns_index

1. First, create FacetGrid
   • df = cf[cf['Val'].isin(['val_1', 'val_2'])]
g = sns.FacetGrid(df, col="Val",col_wrap=6)
   • g= sns.FacetGrid(df, row = 'Val_1', col = 'Val_2' ‘Val_1’ and ‘Val_2’ are two conditions of X
   • g= sns.FacetGrid(df, row = 'Val_1', col = 'Val_2', row_order = ['row_1','row_2'], col_order = ['col_1','col_2','col_3'] give the order for row and col
2. Second, use map object method to plot the data into the laid-out grid
   • g.map(sns.kdeplot,'X')

4.2. Pair Plot

• Default pairplot return scatter plots in the main entries and a histogram in the diagonal.
  • sns.pairplot(df[['X1Y3','X2Y2','X3Y1']])

5. Multivariate Plotting

3.8. sns.lmplot

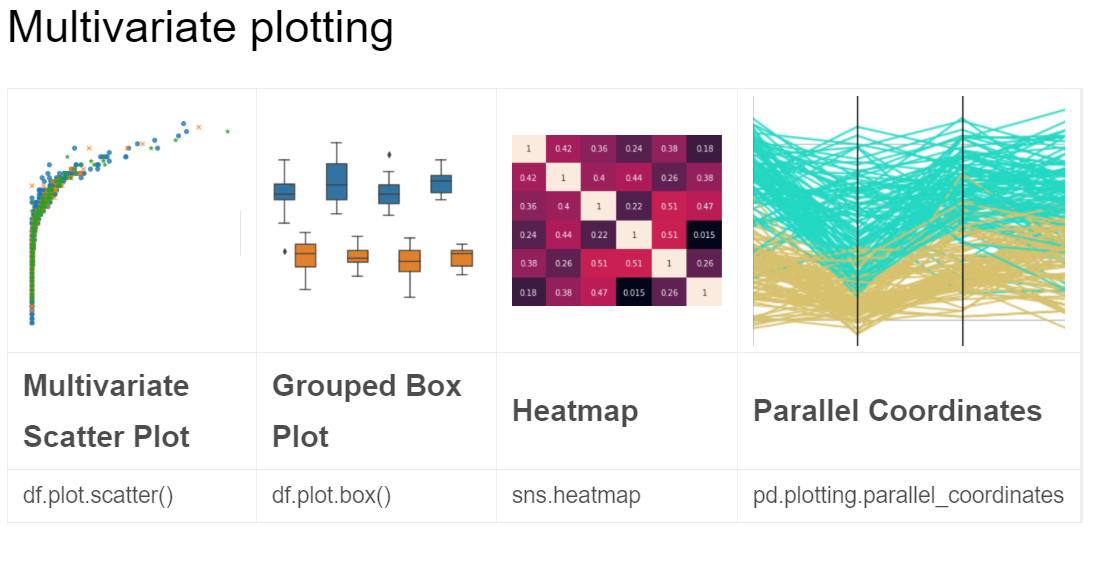
5.1. Grouped box plot

• The main difference is the hue to group two variables into one figure
  sns.boxplot(x='X', y='Y', hue='Val', data=df)

5.2. Heatmap

3.6. sns.heatmap

• ef = (df.loc[:,['Val_1','Val_2','Val_3','Val_4','Val_5']].applymap(lambda v: int(v) if str.isdecimal(v) else np.nan).dropna()).corr()   
  sns.heatmap(ef, annot = True)  
  

5.3. Parallel Coordinates

from pandas.plotting import parallel_coordinates  
ef = (df.iloc[:,12:17].loc[df['Val'].isin(['val_1','val_2'])].applymap(lambda v: int(v) if str.isdecimal(v) else np.nan).dropna())  
ef['Val'] = df['Val']  
ef = ef.sample(200)  
parallel_coordinates(ef,'Val')

6. Plotly

seaborn and pandas focus on building ‘static’ visualizations
plotly is an open-source plotting library which has moving parts

from plotly.offline import init_notebook_mode, iplot  

init_notebook_mode(connected=True)  

import plotly.graph_objs as go  

6.1. go Scatter

iplot([go.Scatter(x=df.head(1000)['X'],y=df.head(1000)['Y'],mode='markers')])

6.2. go Heatmap

iplot([go.Histogram2dContour(x=df.head(500)['X'],y=df.head(500)['Y'],contours=go.Contours(coloring='heatmap')),go.Scatter(x=df.head(1000)['X'],y=df.head(1000)['Y'],mode='markers')]) 

6.3. go Choropleth

df = df['country'].replace('US','United States').value_counts()  
iplot([go.Choropleth(locationmod = 'count')]) 

6.4. go Surface

df = df.assign(n=0).group(['X','Y'])['n'].count().reset_index()   
df = df[df['Y']<100]  
df = df.pivot(index='X', columns = 'points', values = 'n').fillna(0).values.tolist()  
iplot([go.Surface(z=v)])  

7. Grammar of Graphics

from plotnine import *  

Top5_Val = df[df['Val'].isin(df['Val'].value_counts().head(5).index)]  

df = Top5_Val.head(1000).dropna()  

7.1. Scatter plot

(ggplot(df) # initialize the plot with input data df  
	+ aes('X','Y') # aes(aesthetic)  
	+ geom_point() # plot type  
	)  

7.2. Add regression line

(ggplot(df) # initialize the plot with input data df  
	+ aes('X','Y') # aes(aesthetic)  
	+ geom_point() # plot type scatter  
	+ stat_smooth() # add a regression line  
	)

7.3. Add color

(ggplot(df) # initialize the plot with input data df  
	+ geom_point() # plot type scatter  
	+ aes(color='X') # color the X variable points  
	+ aes('X','Y') # aes(aesthetic)  
	+ stat_smooth() # regression line  
	)

7.4. Add facet

(ggplot(df) # initialize the plot with input data df  
	+ geom_point() # plot type scatter  
	+ aes(color='X') # color the X variable points  
	+ aes('X','Y') # aes(aesthetic)  
	+ stat_smooth() # regression line  
	+ facet_wrap('~Var') # facet wrap Variable  
	)

7.5. Aes

aes can be writed as a layer parameter

(ggplot(df)  
	+ geom_point(aes('X', 'Y'))  
	)  

also in overall data

(ggplot(df, aes('X', 'Y'))  
	+ geom_point()  
	)  

7.6. Bar plot

(ggplot(Top5_Val)  
	+ aes('X')  
	+ geom_bar() # bar plot  
)  

7.7. histogram

(...  
	+geom_histogram(bins=20) # numbers of bins  
)  

7.8. 2D histogram

(ggplot(Top5_Val)  
	+ aes('X','Y')  
	+ geom_bin2d(bins=20) # numbers of bins  
	+ coord_fixed(ratio=1) # box height  
	+ ggtitle("Top Five Most Common Vals" # give it titles  
	)  

8. Time-series plotting

pandas.Period

The two most common and basic ways to show up the datas

It often used on stock prices

stocks = pd.read_csv("../input/prices.csv", parse_dates=['date'])  

stocks = stocks[stocks['symbol'] == "GOOG"].set_index('date')  

• line plot visualizing

  shelter_outcomes['date_of_birth'].value_counts().sort_values().plot.line() # output the simple ine plot  
  

• resample

  shelter_outcomes['date_of_birth'].value_counts().resample('Y').sum().plot.line() # aggregated by 'year'  
  

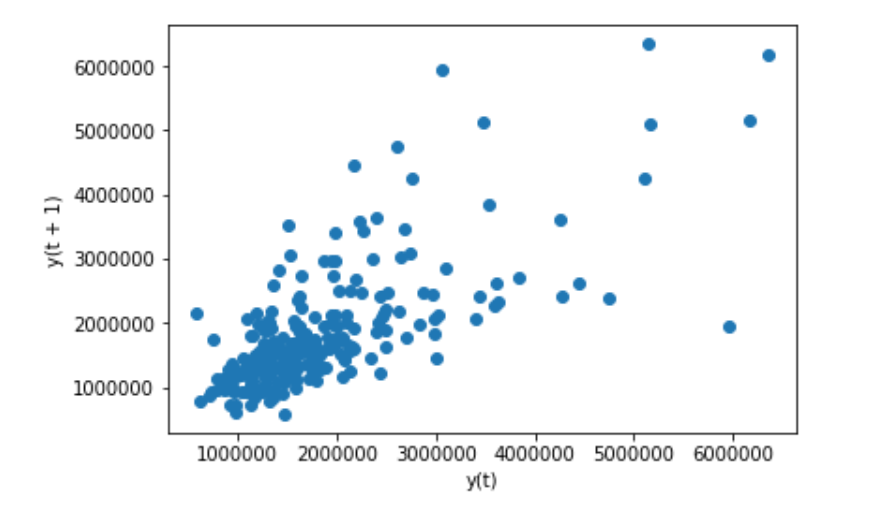
8.1. Lag plot

• A lag plot compares data points from each observation in the dataset against data points from a previous observation

from pandas.plotting import lag_plot  

lag_plot(stocks['volume'].tail(250)) # volume(number of trades conducted)  

8.2. Autocorrelation plot

The autocorrelation plot is a multivariate summarization-type plot that lets you check every periodicity at the same time.
It does this by computing a summary statistic—the correlation score—across every possible lag in the dataset.

from pandas.plotting import autocorrelation_plot  

autocorrelation_plot(stocks['volumne']) # volume(number of trades conducted)  

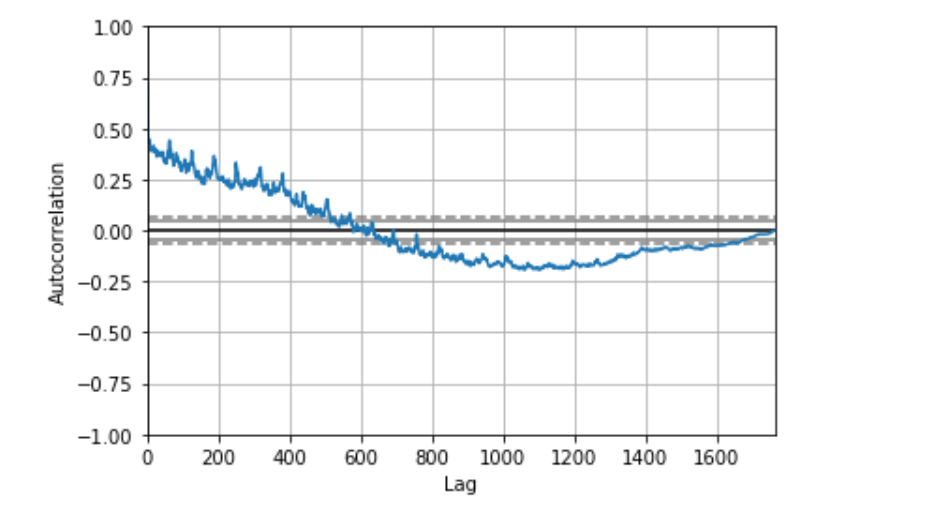
‘The farther away the autocorrelation is from 0, the greater the influence that records that far away from each other exert on one another.

It seems like the volume of trading activity is weakly descendingly correlated with trading volume from the year prior. There aren’t any significant non-random peaks in the dataset, so this is good evidence that there isn’t much of a time-series pattern to the volume of trade activity over time.’